The king comes from a family of 2 children. Assuming that there is an equal probability of a child being a boy or a girl. What is the probability that the other child is his sister?
Hey folks, figures in this article have been featured on Brown University's slide show on Conditional Probability CS145: Probability and Computing (link to lecture 2)
Well this may seem a very simple question on the surface but it manages to capture a very important concept in probability, the famed Bayes' Theorem. In fact, it is a variant of a very controversial question dating back to 1959.
Well this may seem a very simple question on the surface but it manages to capture a very important concept in probability, the famed Bayes' Theorem. In fact, it is a variant of a very controversial question dating back to 1959.
Before we see how this is related to one of the most celebrated theorems in probability and mathematics, what would be you guess?
If you guessed that there was a 2/3 chance that the other child would be a girl then you are right and I assume you understand Bayes' theorem. But if you thought that 1/2 was the correct answer I'm afraid that you might want to look at the drawing board again.
You may have concluded quickly that since the chance of a boy or a girl are equally likely knowing that there is a king in the family doesn't really affect the gender of the other child. How can the gender of one sibling affect that of the other? Or can it?
This is the curious case of conditional probability. "The king comes from a family of 2 children", this statement holds the key. Again, it seems unlikely that this could hold extra information, but actually, it does. The statement gives us two very important pieces of information as you might have guessed already:
1. There are two children in the royal family.
2. There is a king i.e. there is at least one boy in the family.
The pieces seem very obvious but there's nothing extraordinary about them. But if we combine the two pieces something emerges that makes us want to change our belief about the probability of the other sibling being a girl.
Since, here we have a small sample space let's try to enumerate them. Let's assume that we don't have any information as of now. We just know that the royal family has two children. Let's first try to visualize the distribution of the possibilities.
Fig. Sample space S = {BB, BG, GB, GG} without any extra information
For convenience let's denote a Boy with a B and a girl with a G. Our sample space,
S = {BB, BG, GB, GG}
and the chance of any of these four cases of two boys, a boy and a girl, a girl and a boy and two girls is equally likely with probability 1/4.
But when we know that one of the siblings is a boy the sample space changes. We no more have the possibility of having 2 girls in the royal family and we are just left with 3 possibilities in the sample space,
S' = {BB, BG, GB}
Fig. Sample space S' = {BB, BG, GB} given that at least one of the children in a boy
Now we want to know what is the chance of the other sibling being a sister given that we have a king (boy) in the family and this is where the Bayes' theorem comes into play.
The Bayes’ theorem describes the probability of an event occurring given some conditions. This is what the Bayes’ theorem looks like in notation,
P(A|B)=P(AB)P(B)
P(A|B) denotes the probability of event A occurring given event B has occurred. While P(AB) denotes the probability of both event A and B occurring together.
Here, event A is the other sibling being a girl and event B is that at least one of the children is a boy.
Then,
=P(other child being a girl and there is at least one boy in the family of 2 children)/P(there is at least one boy in the family of 2 children)
=(2/4)/(3/4)
=2/3
Looking at it from the perspective of cardinality of the new sample space S' = {BB, BG, GB} that captures the 2 pieces of information that one of the children is a boy. Now, we want to find the probability of the other child being a girl we have 2 possibilities ({BG, GB}) out of the 3 ({BB, BG, GB}) and gives the same result as we got before. Note that this answer is only valid in countries with male-preference primogeniture. In countries such as Sweden with absolute primogeniture, the king can't have an older sister: that is, (g,b) is not a possible outcome, so then the probability is 1/2.
So the next time someone asks you a seemingly straightforward question, there is a chance that Bayes' theorem may help you understand conditioning and come up with the correct solution. Such questions go on to show that there might be more information out there, than we expect. Hopefully, it may help you win Let's Make a Deal, solve some Artificial intelligence problems, make a fortune by predicting the stock market or at least make understanding conditional probability relatively easy.
So the next time someone asks you a seemingly straightforward question, there is a chance that Bayes' theorem may help you understand conditioning and come up with the correct solution. Such questions go on to show that there might be more information out there, than we expect. Hopefully, it may help you win Let's Make a Deal, solve some Artificial intelligence problems, make a fortune by predicting the stock market or at least make understanding conditional probability relatively easy.


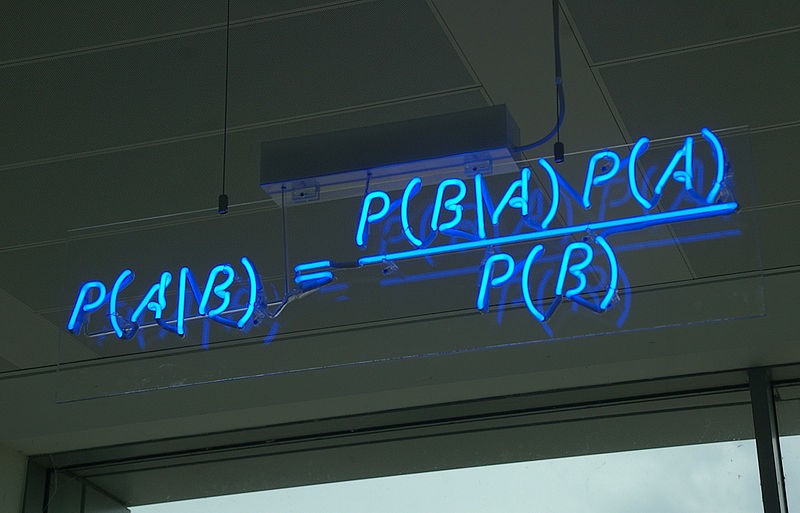
No comments:
Post a Comment