Post content and figures featured on Brown University CS145: Probability and Computing course

What better than being referenced by one of the prestigious university's Probability course. My post that talks about The King's sibling and explaining the Bayes' rule was featured on one of the course material slideshows of the CS145: Probability and Computing, Lecture 2 that can be found here (http://cs.brown.edu/courses/cs145/lectures/lec02_conditional.pdf).

Here's the link to the King's Sibling post I had written. Until next time!

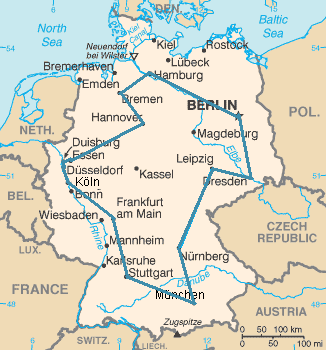
Optimization and Graphs: The travelling salesman problem

The Travelling salesman problem was introduced by William Hamilton. The problem states that you require a Hamiltonian path (a path with no vertices repeated) in a graph so as to minimize the cost/distance function. It is a NP hard problem.

TSP on the major cities in Germany

You may want to keep in mind that using brute force for such problems may take infinite time to run to completion since there are at least N! possibilities for traversing the graph with N nodes (the cities). So you can use some searching informed techniques.

An approach that could prove helpful is start from a node, keep traversing the next closest/cheapest node until you have traversed all the nodes. Then use stimulated annealing with different temperature changing functions (linear, exponential and so on) to get an improved version of your initial feasible solution. This method first finds a feasible solution (in accordance with the problem statement) and then constantly improving the solution and finding an approximated solution in case of very large number of nodes.

You could also attack the problem by constructing solutions which are minimized during the construction itself, but that may prevent you from getting a feasible solution if the conditions aren't checked.

Also you can use techniques such as k-opt or a pairwise swap of edges in the graph genetic algorithms, simulated annealing, Tabu search or ant colony optimization. Hybrid techniques that use more than one of the above techniques usually proves to be more efficient and accurate.

Mind-blowing optical Illusions explained: What is anamorphism?

Given that you've made it this far, first have a look at what this article is all about.

Anamorphosis is a way of projecting an image in a distorted manner so as to convey the actual image by making the viewer take a specific vantage point or in some cases with special optical devices (like a mirror).

The word "anamorphosis" is derived from the Greek prefix ana-, meaning back or again, and the word morphe, meaning shape or form.

There are two main types of anamorphosis:

1.Perspective (oblique)

2.Mirror (catoptric)

Perspectival anamorphosis date to the early Renaissance and are now a major part of various industries, especially advertisement. Mirror anamorphosis were first created in the later. A mirror is placed in proximity of the painting or illustration and if viewed from specific angles it transforms the distortion into an image.

This occurs mainly due to the difference in perspective we get from viewing it from a vantage point compared to a normal place.

The main calculations are done by adjusting the perspective of the image in various software. Various techniques of projection are used to estimate the position and the size of the actual graphic ( illustration). The the angle and the distance from the viewing point are some of the things taken into consideration.

The system of anamorphic projection can be seen quite commonly on text written at a very flat angle on roadways, such as "Bus Lane" or "Children Crossing", which is easily read by drivers who otherwise would have difficulty reading as the vehicle approaches the text; when the vehicle is nearly above the text, its true abnormally elongated shape can be seen.

Also a lot of sports have their fields painted or a printed mat is used instead. It is used to promote brands and when viewed from a specific angle i.e. usually the point-of-view of the camera the image is seen in its undistorted form.

Much writing on shop windows is in origin anamorphic, as it was written mirror-reversed on the inside of the window glass. Ambulances with AMBULANCE written as a mirror image is one of the most common forms of anamorphism.

An anamorphic fresco by Andrea Pozzo at the Church of St.Ignazio.

We like to think of viewing as perception or reality. Our eyes provide continuous raw input to the brain. Since we are accustomed to viewing objects as normal entities and quickly search for familiar patterns like rectangles, squares, circles and try to make something out of what we see. These distortions force our brain to interpret the way we see the actual world and hence the illusion.

We possess something called the "binocular vision" and it's unlike a camera. We fundamentally receive information from a pair of eyes and this creates a alternated view of reality which helps in analysing depth and distance and also anamorphic illusions. The "Ames Room" illusion brilliantly exposes the kind of expectations that we automatically apply to what we see.

Algorithms and Computer Science

Why is computer science a science?

What is the difference between say Physics or Biology and Computer Science? Is there a difference at all?

Well for starters science constitutes of experimentation which makes if fundamentally difference from other subjects that may seem similar at first glance. The field of computer science is a machine science. It deals with a particular type of machine that we colloquially refer to as a PC or a personal computer. So why don't we have something like a tube-light science or a pressure cooker science?

That is something debatable but computers unlike a tube-light or a pressure cooker doesn't inherently have a singular purpose such as glowing or boiling your favourite veggies. If you can encode your thoughts in a precise and particular manner, the personal computer can function based on that. These may vary from solving problems that occur while studying particle physics and trying to make sense of the humongous amount of variegated data or as inconsequential as calculating the amount you spent on groceries at the market.

Alan Turing, the father of theoretical computer science wrote a scientific paper in which he described "computers" as people (mostly women at that time, primarily due to their patience while performing arduous calculations) who did math on pen and paper according to the whims of a set of sequential instructions also known as an algorithm.

Let's go back to the pressure cooker. 

Could there be a microwave oven science, since we already have one that caters to a pressure cooker? What cooks faster in a pressure cooker: a chicken or some potatoes? Potatoes or rice? Rice or wood? Wood or Iron? That escalated quickly.

On closer observation, there seems to be some sort of classification. Things that cook slow, other food items that cook quicker and some others, even quicker. And then there's this class of items that are so stubborn that they won't boil in a pressure cooker, like a piece of metal. Every science begins with classification and so does the one that deals with theoretical computer science.

Absurd as it may sound, in this context, we are dealing with the contents or what we can actually come up with, rather than the tool itself. We are worried about the chicken or the rice or perhaps the potatoes in the cooker rather than the humble pressure cooker itself. Similarly theoretical computer science at it's heart doesn't believe in discriminating based on the tool we use, whether it's a microwave oven or an old school pressure cooker, all we are worried about is getting nice boiled potatoes in the end. It doesn't really matter whether you have a super computer of this generation or a quantum technology powered device of the next era. This is what is computational complexity.

Things cooking at various speeds can be compared analogously to the various complexity classes in computer science, that instead of rating food items classify algorithms on their efficiency for easy comparison and deciding what maybe difficult for a computer to solve.

Difficulty is relative. Someone may find talking to a girl really difficult while another one may deem waking up early in the morning a difficult task. Many may also find it laborious to prove the Pigeon-hole principle. Computer science calls problems difficult that require at least exponential number of steps in the size of an input to an algorithm. But a database scientist may treat anything worse than a logN or a linear algorithm as inefficient. Depending on the context the definition of hardness may vary. The algorithms are compared in terms of the number of instructions required, space occupied (as a scratchpad), etc. These metrics are technology independent and that's where the universality lies. You'd compare them in the next century as you would in this. Doesn't matter what kind of specification the system has. The tool is just a means, it's the method that we bother about.

While mathematics has this puzzle kind of perspective to it. If you have solved a jigsaw puzzle or say a Rubik's cube, which you most certainly have, for the first time it may seem more of a challenge. But once you know how a jigsaw puzzle works and understand the concept behind it, you can solve any puzzle with the same technique. If you know how to computer 33+12, you can surely compute 132144+39427438 with little difficulty. Once a mathematical problem is solved, it is like you've become aware of the great magician's secret. Any local fair you visit and you see a person performing the trick you'll be aware of how it's done, irrespective of whether it's happening.

A solution for the travelling salesman problem for the cities in Germany.

On the other hand, computer science deals with skewing the problem. Let's say that now you take a 4x4 Rubik's cube to solve. What happens to your step-wise procedure? Does it work as expected or fails miserably? What happens to the number of steps when you consider a cube of an arbitrary size NxN? How much space does the computer need as a scratch pad to find a conclusive solution? Here, as soon as you fish out an algorithm it is then that you have even more questions to answer than you had to begin with in the first place.

P.S.: I attended a talk on algorithms and this is what it was all about. Really simple stuff but made a lot of sense. I thought I'd share it with my readers. :)

The Number Revolution: How math explains our world

Russian physicist Igor Tamm won the Nobel Prize in physics in 1958. During the Russian revolution, he was a physics professor at the University of Odessa in the Ukraine. Food was in short supply, so he made a trip to a nearby village in search of food. While he was in the village, a bunch of anti-communist bandits surrounded the town.The leader was suspicious of Tamm, who was dressed in city clothes. He demanded to know what Tamm did for a living. He explained that he was a university professor looking for food. “What subject?,” the bandit leader asked. Tamm replied “I teach mathematics.”“Mathematics?” said the leader. “OK. Then give me an estimate of the error one makes by cutting off a Maclaurin series expansion at the nth term. Do this and you will go free. Fail, and I will shoot you.”Tamm was not just a little astonished. At gunpoint, he managed to work out the answer. He showed it to the bandit leader, who perused it and then declared “Correct! Go home.” Tamm never discovered the name of the bandit.

From “Calculus makes you live longer”, in “100 Essential Things You Didn’t Know You Didn’t Know”, by John Barrow

Nobody can promise that math may save your life but it can certainly change it. Almost everyone who takes one math class or the other usually ends up describing the class as a collection of obscure symbols and gibberish.  Many of the younger students even end up developing a feeling of hatred towards the subject.  Maybe if given a different perspective of the subject they may have a different outlook on it altogether.

Would you like to know the future? How life started or something as trivial finding out what’s on tomorrow’s routine test? How could anyone possibly know that? What if there was something that contained all the information that was, is or will ever exist?

​

Pi knows it all. 

Pi is omniscient. The number contains a never-ending sequence of all possible digit permutations. Using an elementary computer program one can convert Pi to its ASCII equivalent and that data contains all the information you’d ever want. Doesn’t it sound like the treasure from Robert LouisStevenson’s Treasure Island? The universe and everything in it contained in one never ending trail of digits. Simply ingenious. That’s just the glimpse of the power of numbers. But the ability to yield such power only comes with understanding.

Numbers have been an integral part of humanity since millennia. The need for numbers appeared when man wanted to quantify things; from the cattle he owned, the berries he foraged to the quantification of light.

Math is known for the intrinsic aesthetics. Simplicity and generality are valued. Artists like da Vinci used math for making masterpieces while others used it to find rigorous proofs for things that thrilled them.

One thing led to another. A never ending chain reaction initiated. Along came Aryabhatta (one of the first to use shunya or the zero), Isaac Newton(needs no introduction; key figure in the scientific revolution) , Leonhard Euler (infinitesimal calculus and calculus), John von Neumann (quantum logic, computer architecture and a really long list of equally important achievements), George Boole (pioneer behind Boolean algebra) and a huge group of geniuses that changed our outlook on the world forever. They believed that 'no idea was small'.

There was such a revolutionized way of thinking that numbers were no longer just used to count the dozen bananas you bought or to keep track of the money you spent. Numbers meant more than that. An image is nothing but a sequence of numbers arranged in a particular pattern; numbers could tell if you had cancer by just looking at you, they could compromise a strategic enemy position without spilling any blood. Math can tell you whether tomorrow is a good day to go for a family picnic to Central Park. Numbers can even talk to you and give advice.

Such is the power of mathematics and numbers.

Math has become a really powerful tool. Just as the Neanderthals had their hand-axes, we have math. Math and logic have crept into our daily lifestyle without our noticing and are influencing this planet in a way bigger than we can imagine. With each passing day scientists and scholars are pushing mathematics and taking it to the next level. Almost everything in the world is moving towards digitization. A day will come when the world will be represented by 0's and 1's and numbers shall takeover. This revolution has been taking shape since centuries. Only a question remains. 

Do you want to be a part of the biggest revolution in the history of mankind?

The King's Sibling: How well do you understand probability?

The king comes from a family of 2 children. Assuming that there is an equal probability of a child being a boy or a girl. What is the probability that the other child is his sister? 

Hey folks, figures in this article have been featured on Brown University's slide show on Conditional Probability CS145: Probability and Computing (link to lecture 2)

Well this may seem a very simple question on the surface but it manages to capture a very important concept in probability, the famed Bayes' Theorem. In fact, it is a variant of a very controversial question dating back to 1959.

Before we see how this is related to one of the most celebrated theorems in probability and mathematics, what would be you guess?

If you guessed that there was a 2/3 chance that the other child would be a girl then you are right and I assume you understand Bayes' theorem. But if you thought that 1/2 was the correct answer I'm afraid that you might want to look at the drawing board again.

You may have concluded quickly that since the chance of a boy or a girl are equally likely knowing that there is a king in the family doesn't really affect the gender of the other child. How can the gender of one sibling affect that of the other? Or can it?

This is the curious case of conditional probability. "The king comes from a family of 2 children", this statement holds the key. Again, it seems unlikely that this could hold extra information, but actually, it does. The statement gives us two very important pieces of information as you might have guessed already:

1.     There are two children in the royal family.

2.     There is a king i.e. there is at least one boy in the family.

The pieces seem very obvious but there's nothing extraordinary about them. But if we combine the two pieces something emerges that makes us want to change our belief about the probability of the other sibling being a girl.

Since, here we have a small sample space let's try to enumerate them. Let's assume that we don't have any information as of now. We just know that the royal family has two children. Let's first try to visualize the distribution of the possibilities.

Fig. Sample space S = {BB, BG, GB, GG} without any extra information

For convenience let's denote a Boy with a B and a girl with a G. Our sample space, 

S = {BB, BG, GB, GG}

and the chance of any of these four cases of two boys, a boy and a girl, a girl and a boy and two girls is equally likely with probability 1/4.

But when we know that one of the siblings is a boy the sample space changes. We no more have the possibility of having 2 girls in the royal family and we are just left with 3 possibilities in the sample space,

S' = {BB, BG, GB}

Fig. Sample space S' = {BB, BG, GB} given that at least one of the children in a boy

Now we want to know what is the chance of the other sibling being a sister given that we have a king (boy) in the family and this is where the Bayes' theorem comes into play.

The Bayes’ theorem describes the probability of an event occurring given some conditions. This is what the Bayes’ theorem looks like in notation,

 P(A|B)=P(AB)P(B)

P(A|B) denotes the probability of event A occurring given event B has occurred. While P(AB) denotes the probability of both event A and B occurring together.

Here, event A is the other sibling being a girl and event B is that at least one of the children is a boy.

Then,

P(other sibling being a girl|there is a boy in the family of 2 children)

=P(other child being a girl and there is at least one boy in the family of 2 children)/P(there is at least one boy in the family of 2 children)

=(2/4)/(3/4)

=2/3

Looking at it from the perspective of cardinality of the new sample space S' = {BB, BG, GB} that captures the 2 pieces of information that one of the children is a boy. Now, we want to find the probability of the other child being a girl we have 2 possibilities ({BG, GB}) out of the 3 ({BB, BG, GB}) and gives the same result as we got before. Note that this answer is only valid in countries with male-preference primogeniture. In countries such as Sweden with absolute primogeniture, the king can't have an older sister: that is, (g,b) is not a possible outcome, so then the probability is 1/2.

So the next time someone asks you a seemingly straightforward question, there is a chance that Bayes' theorem may help you understand conditioning and come up with the correct solution. Such questions go on to show that there might be more information out there, than we expect. Hopefully, it may help you win Let's Make a Deal, solve some Artificial intelligence problems, make a fortune by predicting the stock market or at least make understanding conditional probability relatively easy.

Liked the post? Comment about it, share it or check out more on why the Beatles sang what they sang or read how numbers explain our world.